蒙特卡洛方法
核心思想
用随机样本的统计结果去近似一个数学问题的真实答案。
蒙特卡洛求 π
蒙特卡洛求 π 这个例子大学的时候已经学过了,这里就不再讲解。
蒙特卡洛树搜索
Monte Carlo Tree Search
一共4步,如下。
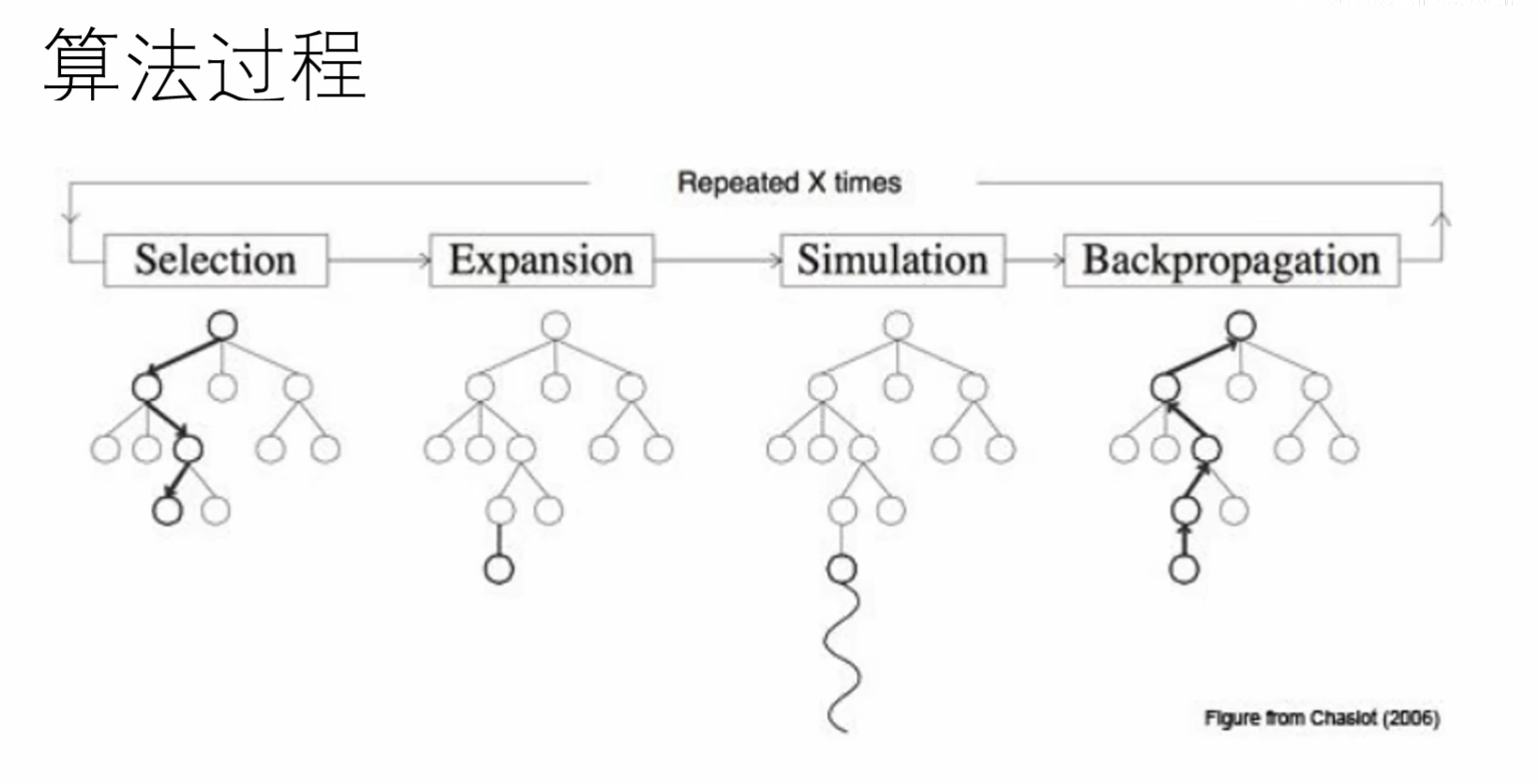
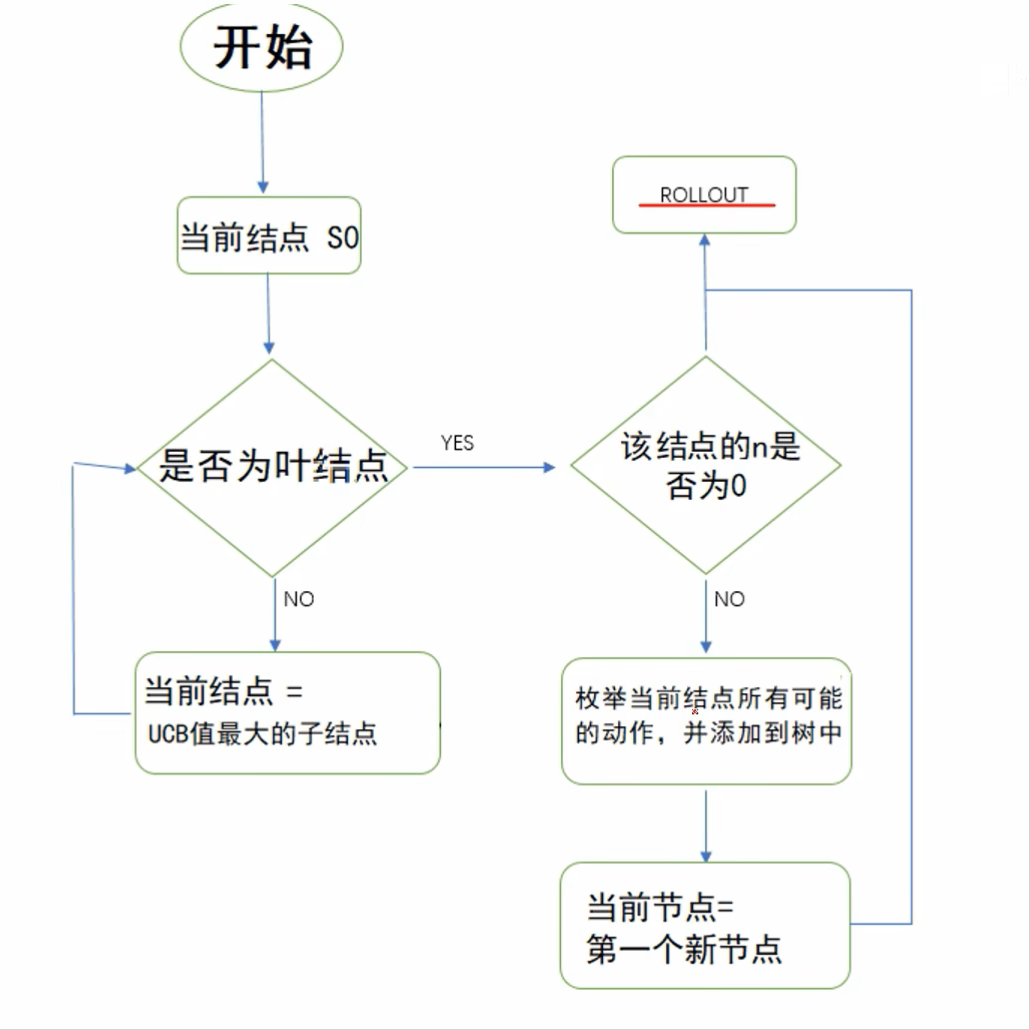
一、selection
用下面公式给每个子节点打分。

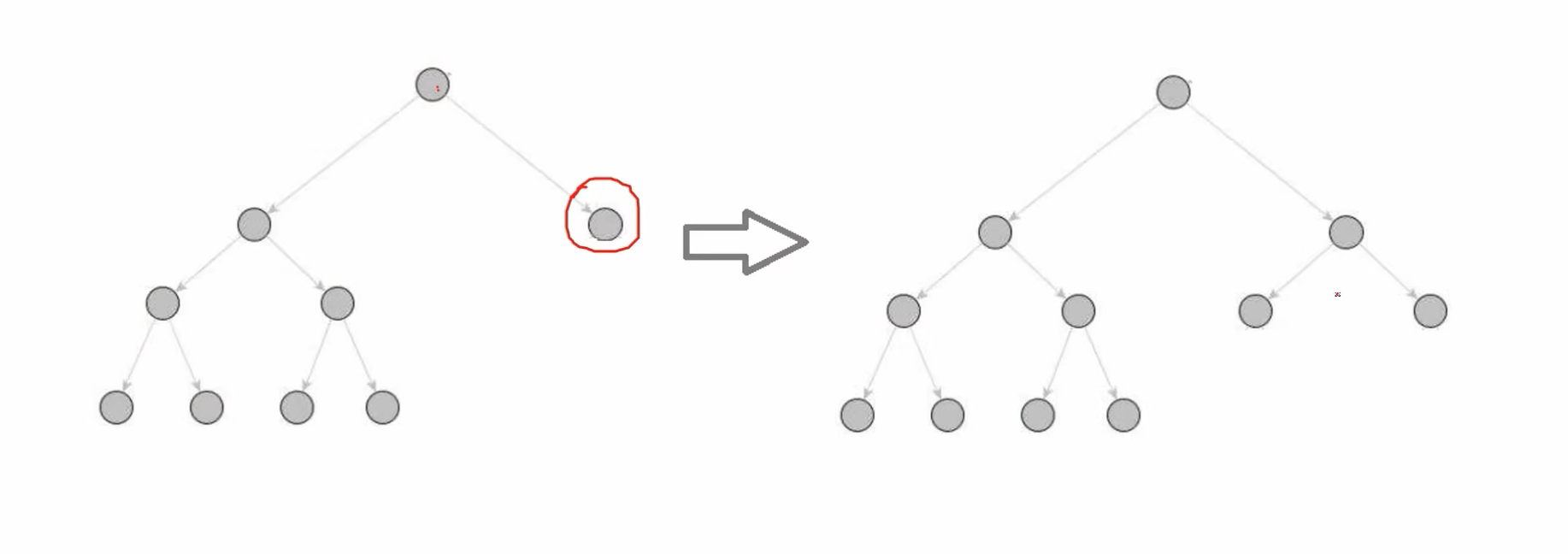
二、node expansion
如果是叶子节点,扩展出新的节点。
三、simulation(仿真)rollout (出品)
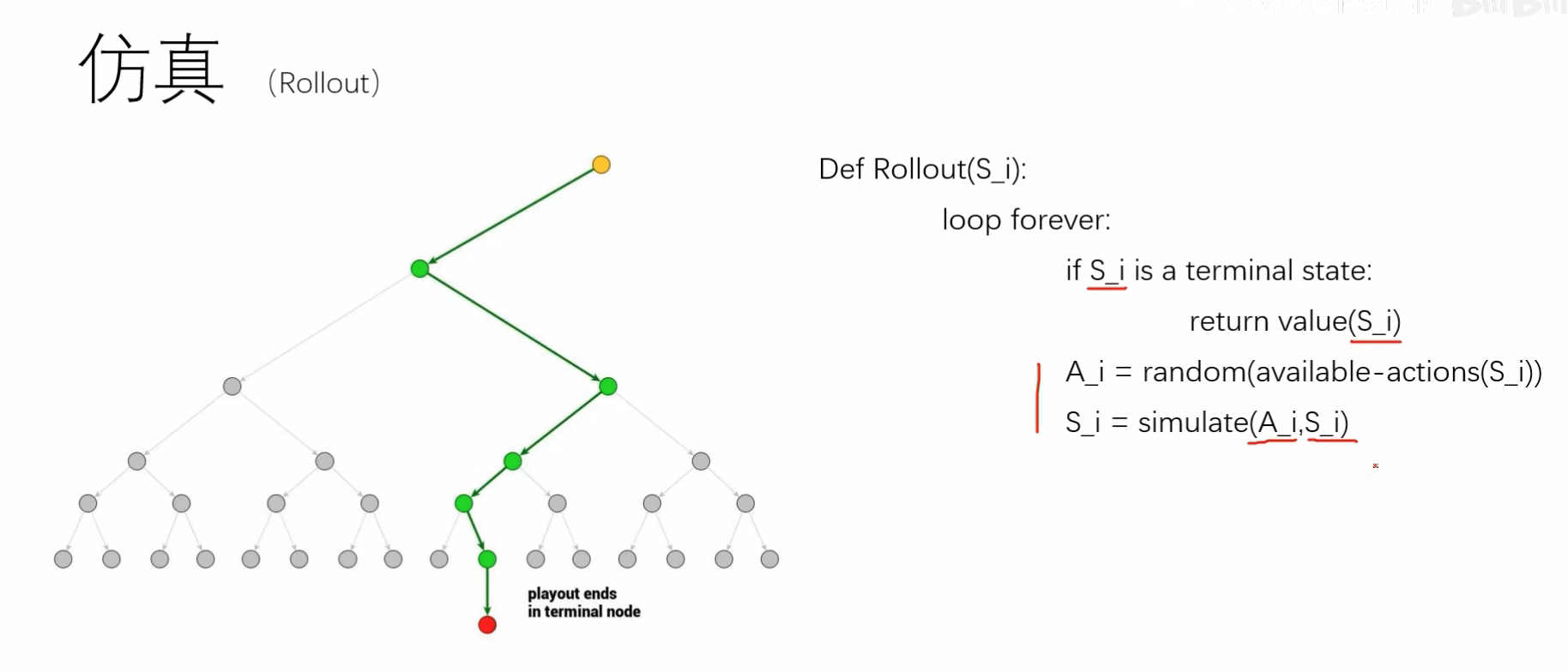
从这个新节点开始,用随机(或启发式)方法“玩”到游戏结束。叶子节点就算是一个游戏结束的状态。
👉 这一步就是应用“蒙特卡洛方法” —– 用随机样本的统计结果去近似一个数学问题的真实答案。
注意,一个非常容易让人误解的点!:
这里的 整个rollout计算过程中,涉及到的行为路径选择 和 terminal state,都是和前文中这个蒙特卡洛树没有关系的,相当于在现在这个状态中又开一局游戏,通过不断的随机操作,来模拟出游戏直到游戏结束,给出我们一个 value 打分!和之前我们建立的蒙特卡洛树是没有关系的!如果说有关系,那就是rollout的初始状态是基于蒙特卡洛树的那个节点的状态。
rollout(模拟)阶段的所有状态变化、随机选择、直到 terminal state 的过程,
都不是蒙特卡洛搜索树(MCTS)中的节点。它们只是一场“基于当前叶节点状态的随机游戏”。
唯一的联系是:
rollout 的起点(初始状态)= 树中刚刚扩展出来的那个叶节点的状态。模拟的结果(value)会反向传播回树里,
更新叶节点及其祖先节点的价值估计。
可以这样理解:
- MCTS 树的作用:保存已经探索过的、较有价值的状态空间(“地图”)。
- rollout 的作用:从“地图边缘”往外随机看看未来会发生什么(“探路”)。
四、back propagation(反向传播)
从 rollout 中找到适合的值,放到树中适合的位置中去。
就是把 value 的值从路径的节点中加一遍。
算法终结
1、限制时间
2、固定迭代次数
结束时选择一个 value 更大的节点完成决策。
例子
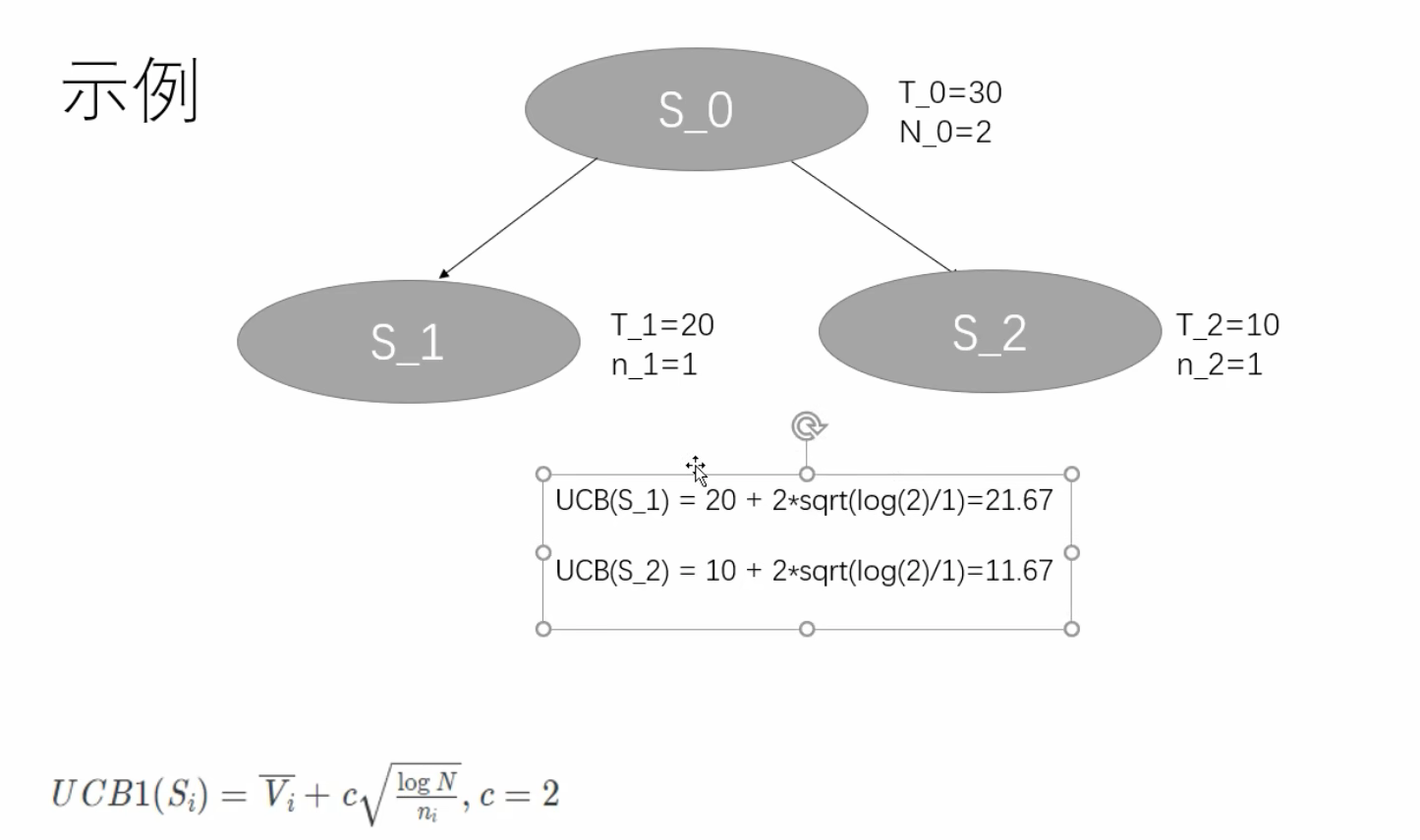
这里的 T 就是 selection 章节中介绍的 value。 N是总探索次数,n是这个节点的探索次数。
初始状态如下,根节点是叶子节点;
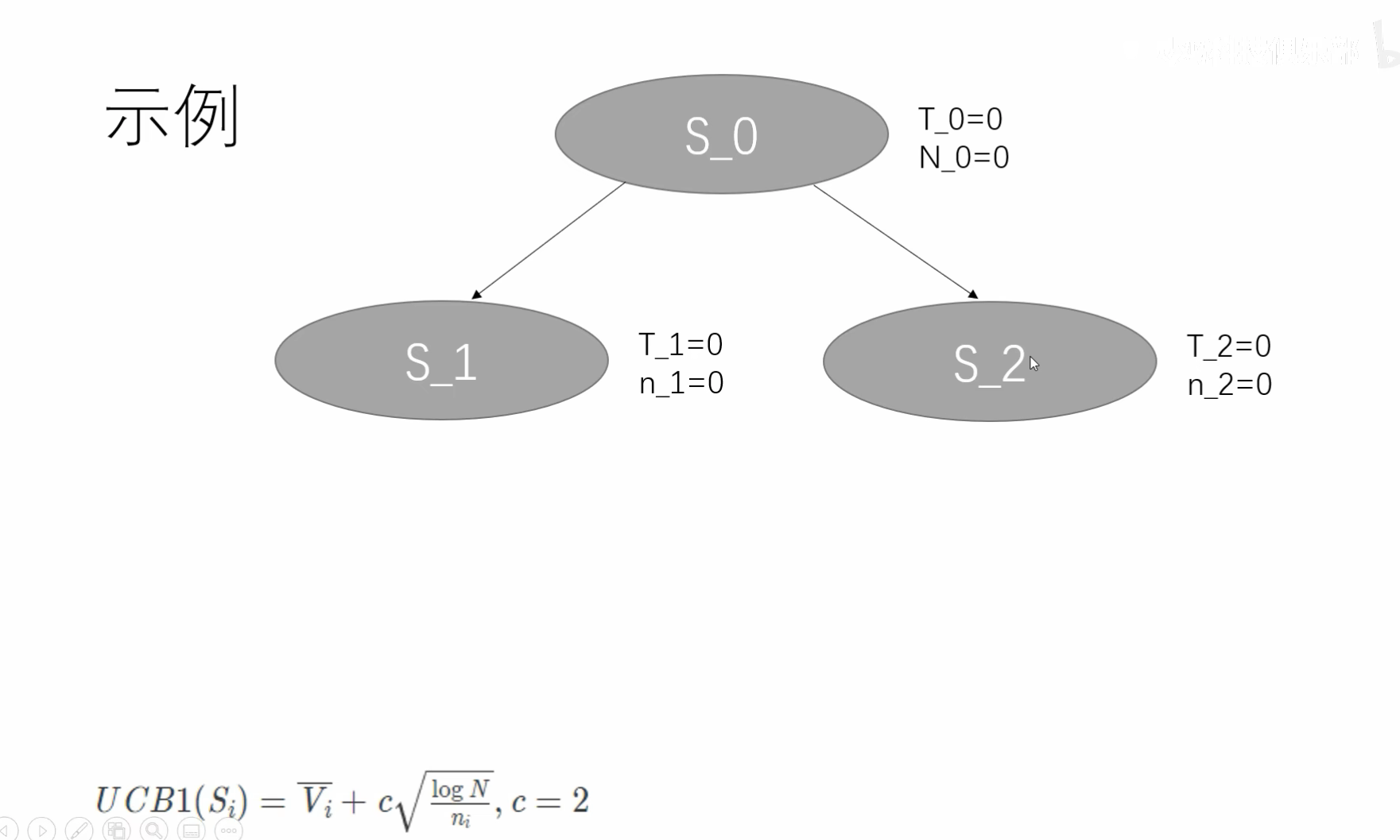
在expansion出两个节点后,发现ni都为0,导致UCB1两个拓展的节点都是∞。所以UCB1是相等的,理论上选谁都一样。
是叶子节点同时又没有被探索过,根据前面的流程图,直接就行 rollout计算。
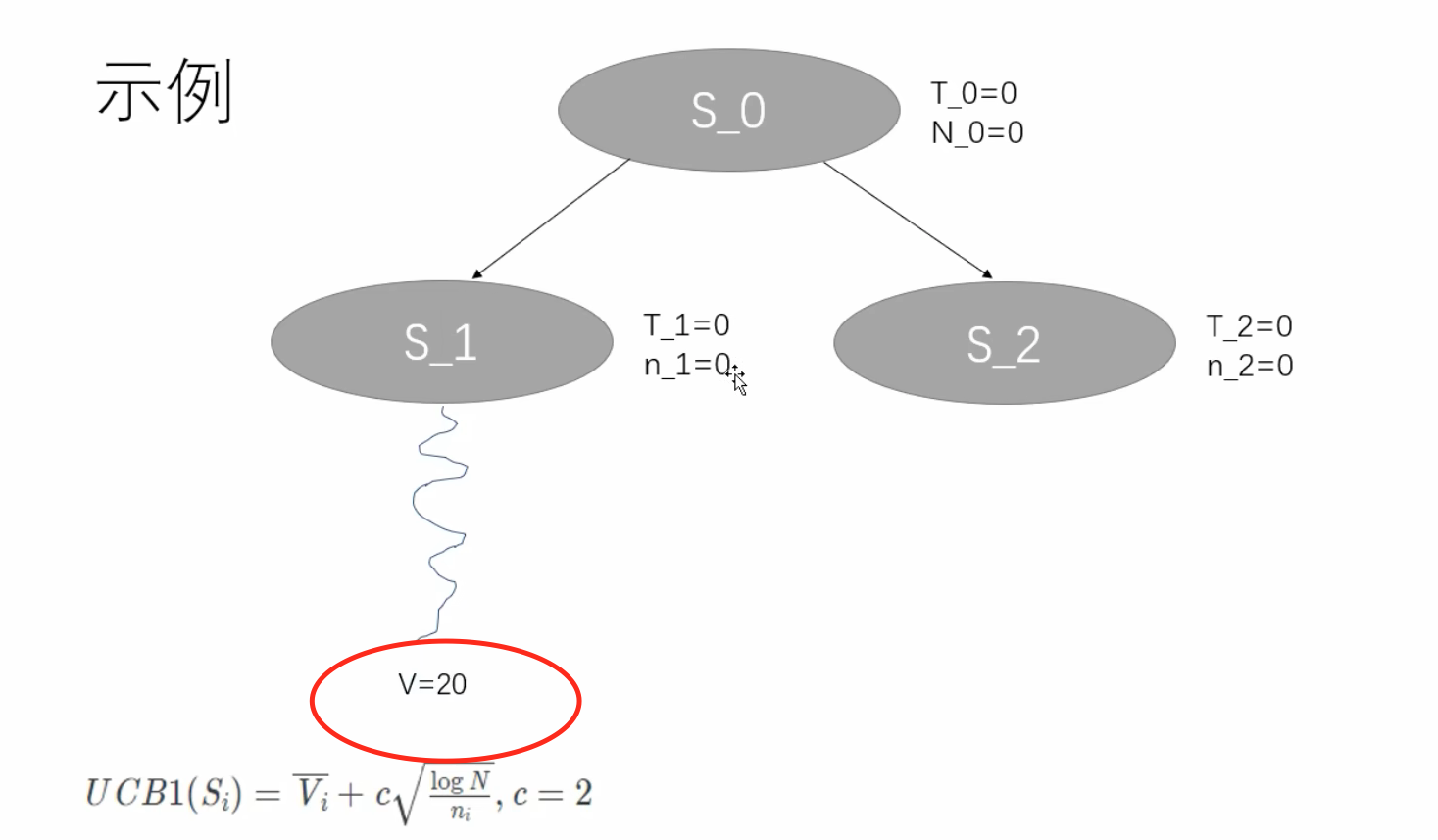
计算出了一个value值,为20 。
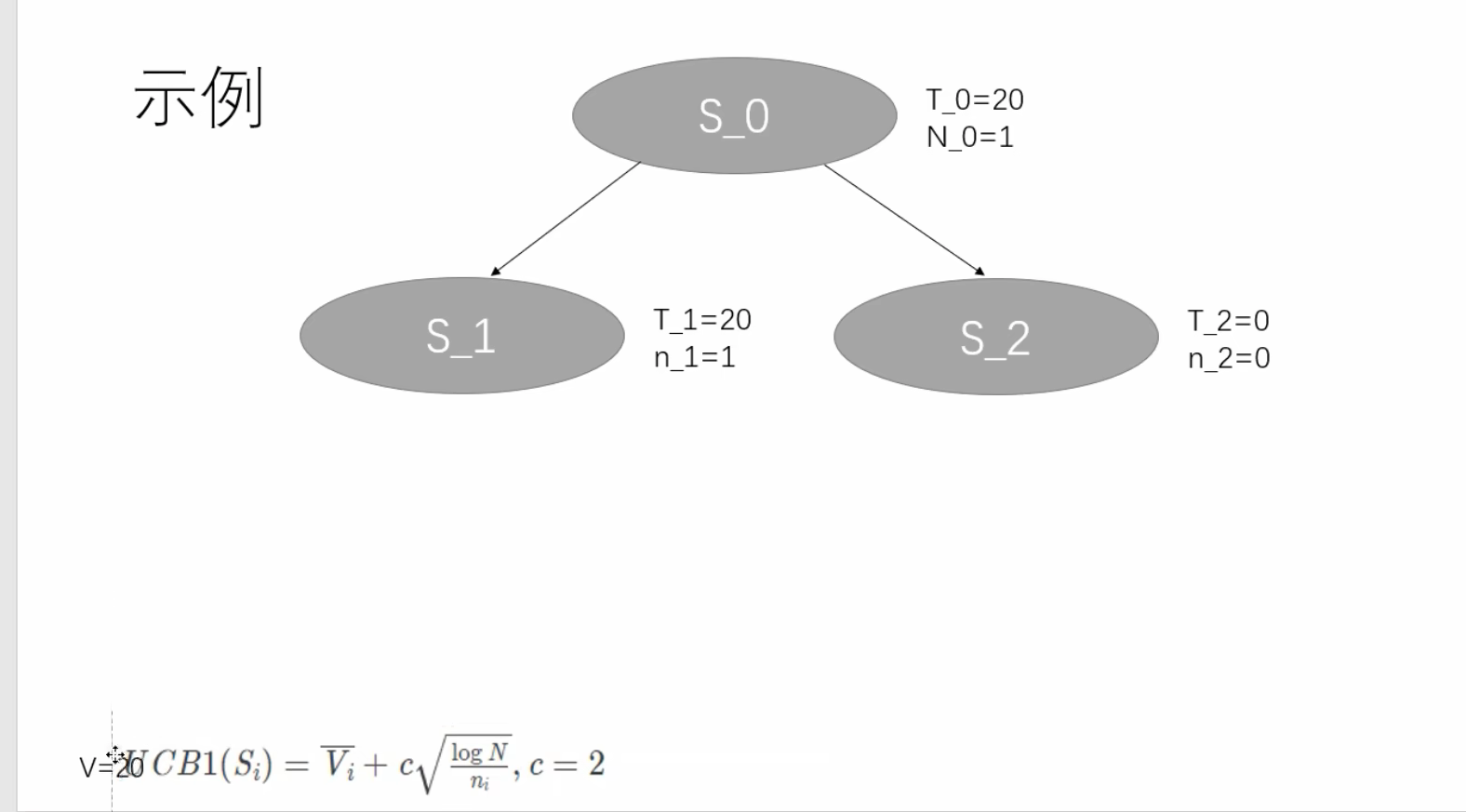
反向传播,把路径上的节点的价值都改成20;N_0 = 1 了,因为被探索过一次了。
此时重新 从根节点出发,再 执行上面的一轮操作,发现 S_1 的UCB1已经是一个固定值了,而 S_2 由于 没有被访问过,这个值还是一个∞,导致了我们一定会选择 S_2 节点。
给 S_2 节点来一轮以后,假如 它的值是 10,则根节点总访问次数会由于反向传播累加,变成2,value累加成20+10=30;
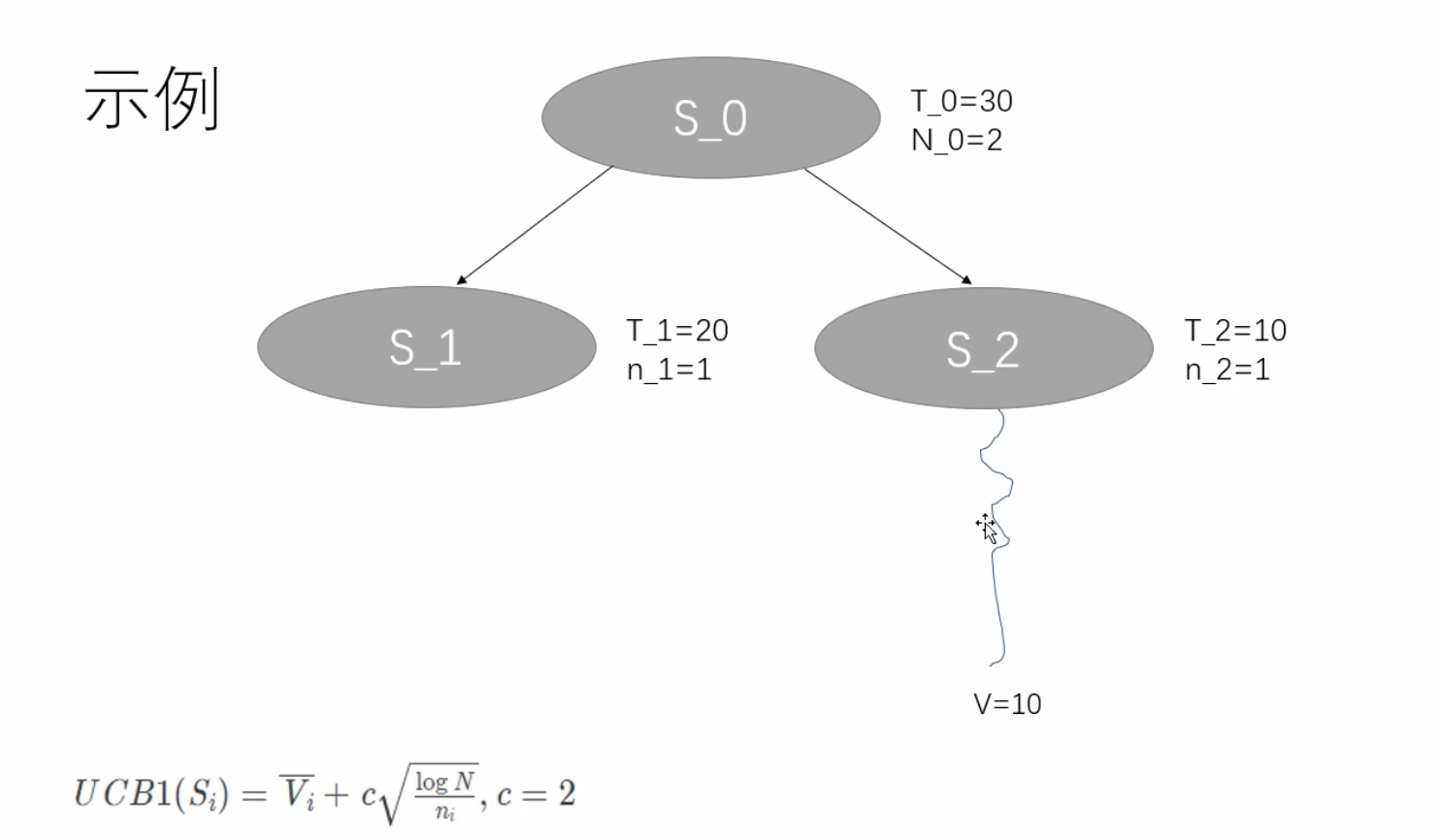
现在开始重新从S_0节点开始第二轮。
算出 UCB 值,给 S_0 的所有子节点打分。
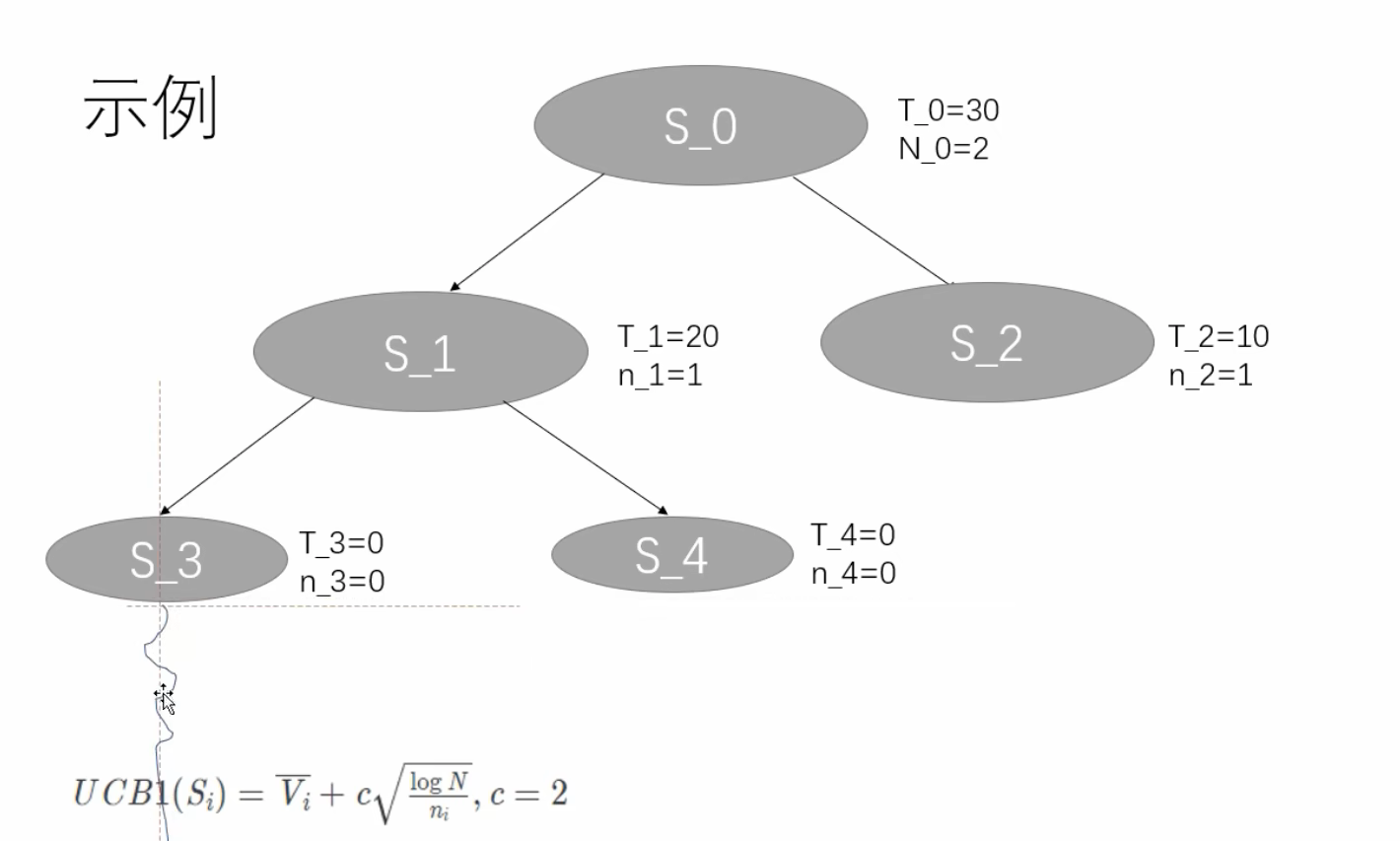
发现 S_1 节点大,所以选择 S_1 ,发现 S_1 是叶子节点,但是已经被访问过了,按照流程给它 枚举所有可能的动作,并添加到树中,然后 当前节点 = 第一个新节点,用这个节点去做 rollout 计算。
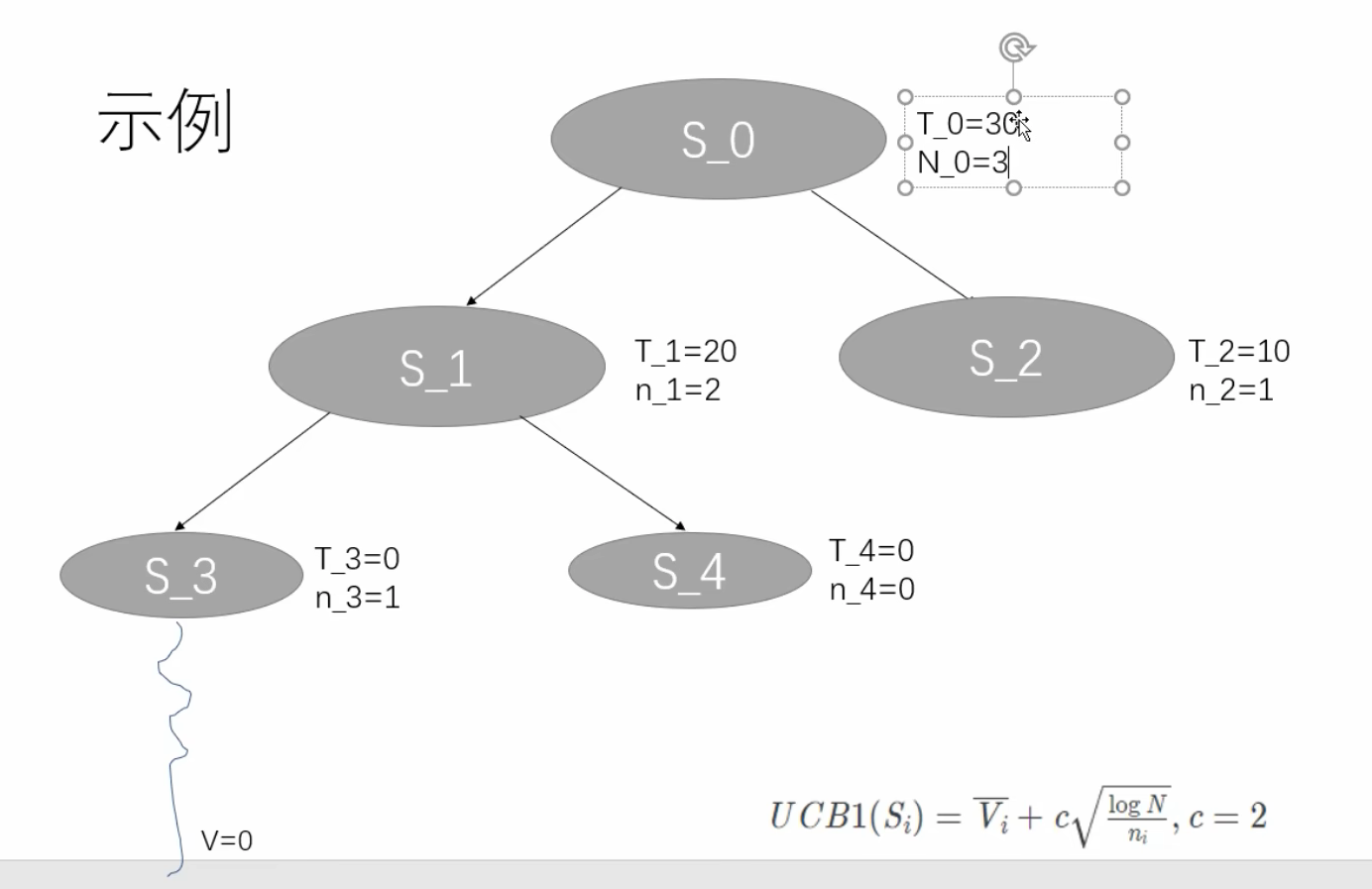
再back propagation;
这一轮执行完毕之后又回到了 S_0 , 此时又重新开始一轮 selection,计算 UCB ,但是需要注意,这个 Vi 是平均值,Vi 的值需要除他的探索次数。
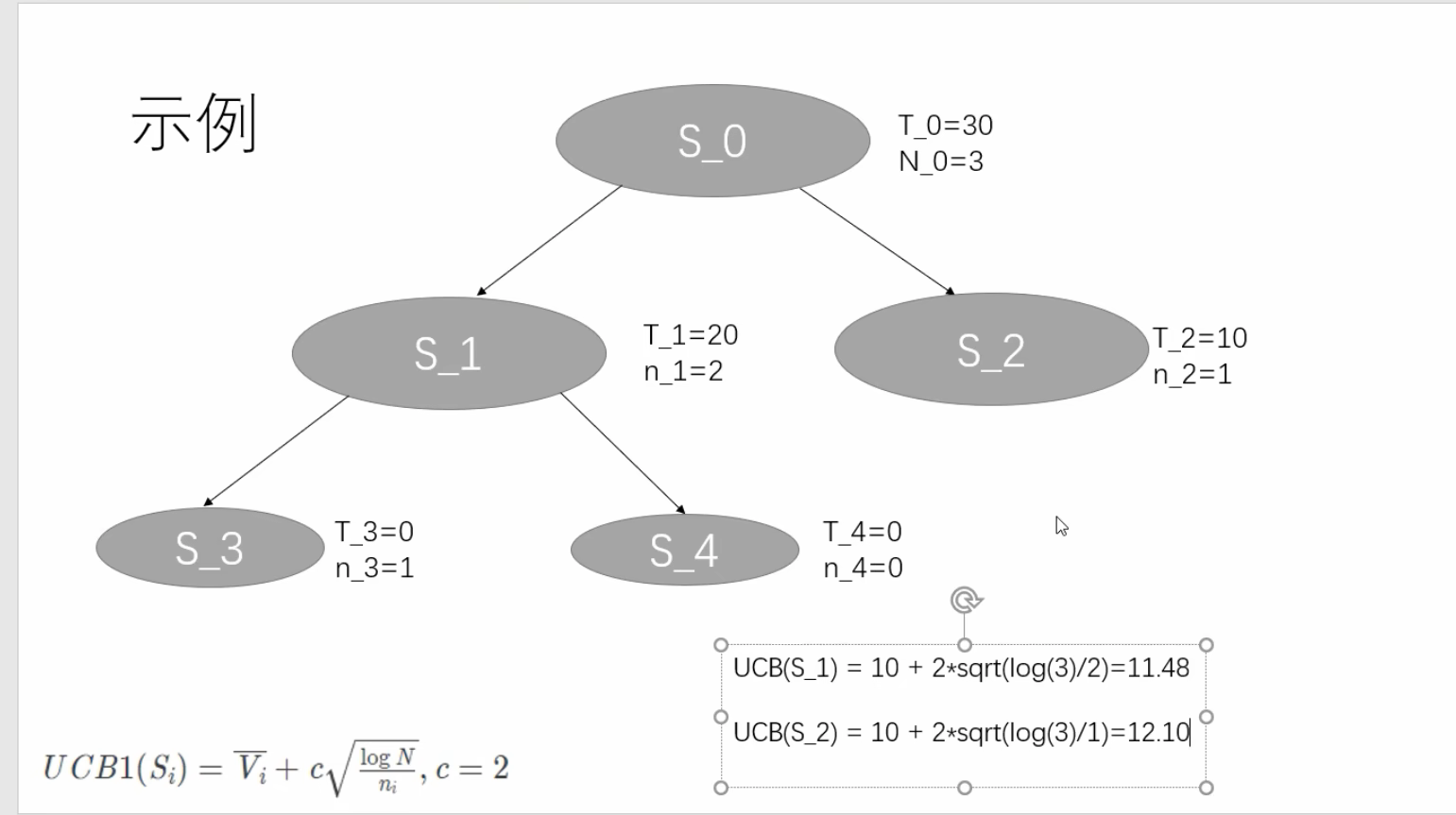
此时 S_2 的值更大一些,所以,我们现在选择的是 S_2 节点;
我们可以发现 S_2 是叶子节点,又被探索过,按照流程,先对它 枚举所有动作加入树中,然后选第一个动作,做rollout计算,再back propagation。
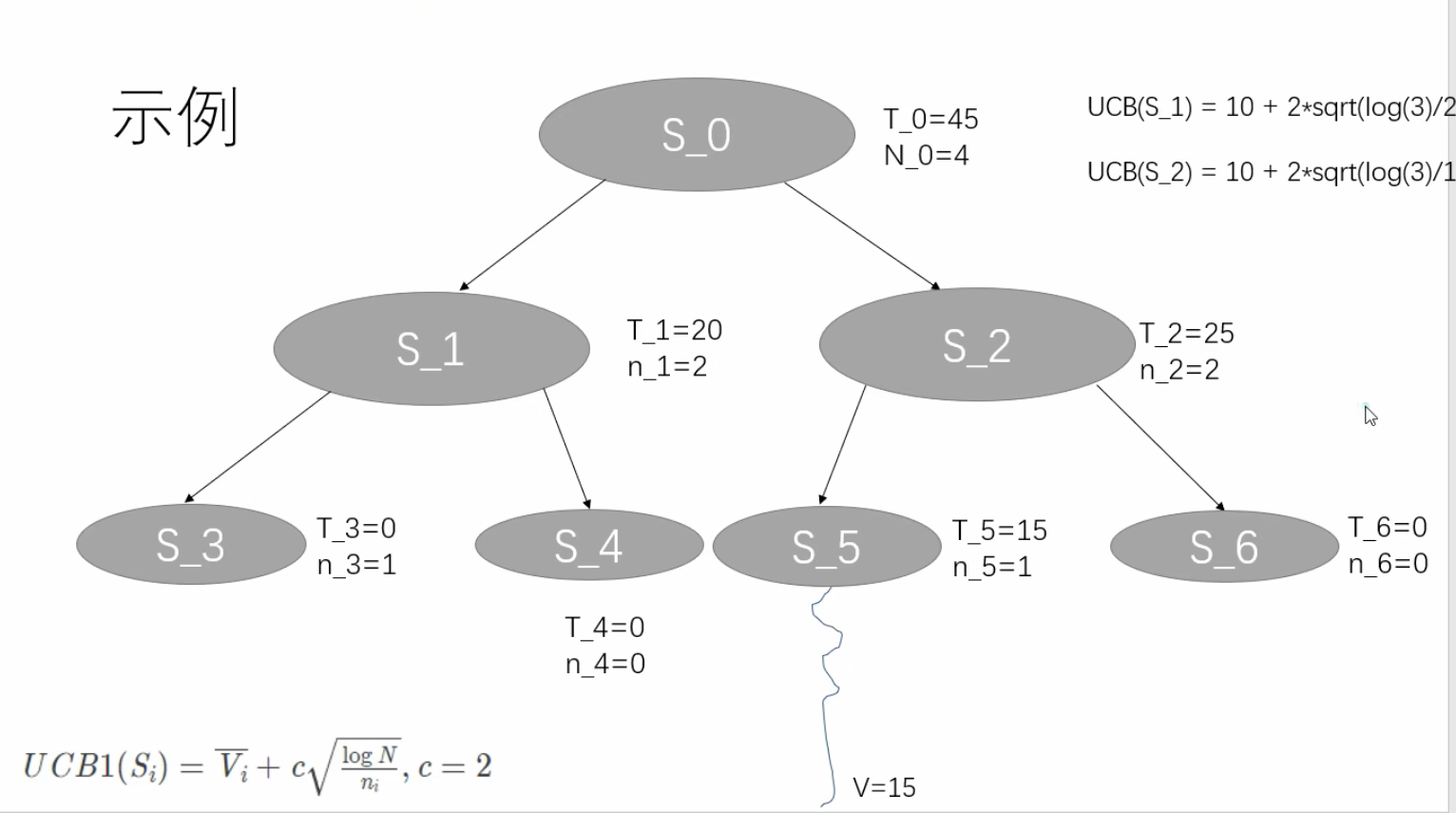
假如我们的程序在此时就停下来了,我们来看看会怎么执行?
由于此时计算 S_1 和 S_2 的 UCB ,会发现 S_2 的更大,所以会选 右边那条路径。
总结
MCTS像一个带反向传播和路径赋值功能的二叉树,但是需要明确的一点是,但它不是固定的「普通二叉树」,而是根据策略动态扩展的「非固定分支搜索树」。
在simulation仿真中,用随机(或启发式)方法“玩”到游戏结束。
👉 这一步就是应用“蒙特卡洛方法” —– 用随机样本的统计结果去近似一个数学问题的真实答案。
MCTS 的思路:
“随机尝试多次,统计哪条路径胜率高,然后优先探索它。”
可以这样理解:
- MCTS 树的作用:保存已经探索过的、较有价值的状态空间(“地图”)。
- rollout 的作用:从“地图边缘”往外随机看看未来会发生什么(“探路”)。
再通过“探路结果”反向传播 回去修正来MCTS树。